|
The two tables below sumarize the probably of drawing x-number of dominos in any suit and in specific suits. A simulated hand of seven random dominos was repeatedly drawn from a shuffled set of double-six dominos. Combinations for the doubles suit were calculated.
Table I shows the results of drawing 100,000 hands for x-number of dominos in any suit. This was done using compuer simulation. Calculation of the values are not shown. If you have the mathematical expressions for calculating the odds of drawing x-number of dominos in any suit and you would like to share them, please contact me, and I will post them for public viewing in this document. Table II shows the odds of drawing x-number of dominos in specific suits, calculated and simulated. The combinations of doubles drawn in a hand were calculated because doubles is a unique suit, and they're easier to work with when applying mathematical expressions involving factorials. Once the logic for possible combinations was determined, it was relatively easy to calculate the odds of drawing a hand of dominos with those exact combinations. To verify the calculated results in Table II, I ran 100,000 iterations in a computer program to tabulate the number of times that exact combinations of suits in a seven-domino hand were drawn from a shuffled pool of 28 dominos. The results for doubles matched the calculated values. The results also showed the combinations applied to the other seven suits as well. So, based on this finding, I included the other suits in the table. The probabilities for the specific suits and their simulated verifications are shown following the calculations. Empirical data are also shown for the hands randomly drawn by the computer.
, webmaster
|
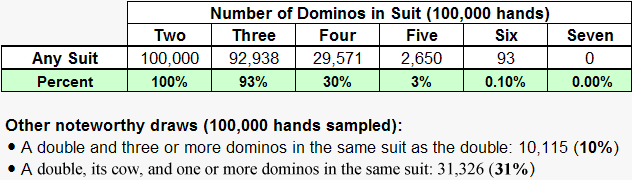
| Number of Dominos in Any Suit 2 | Odds of Drawing (Rounded) | Probability (Rounded) |
| Two or more | 1 in 1 | 100% 3 |
| Three or more | 1 in 1 | 93% 4 |
| Four or more | 1 in 3 | 30% |
| Five or more | 1 in 38 | 3% |
| Six or more | 1 in 1075 | 0.1% |
| Seven | 1 in 148,005 5 | 0.001% |
| OTHER ODDS IN DRAWING | ||
| Both ten-count dominos (6-4 and 5-5) | 1 in 18 6 | 6% |
| A double and three or more dominos in the same suit as the double | 1 in 10 | 10% |
| A double, its cow,7 and one or more dominos in the same suit as the double | 1 in 3 | 31% 8 |
| Notes:
1. The number of possible combinations for drawing seven-domino hands is 1,184,040. 2. There are eight possible trump suits: blanks, aces, deuces, treys, ..., sixes, doubles. 3. The odds of drawing two dominos in any suit is 99.9999% (1 minus 1/1,184,040). 4. The odds of drawing three dominos in any suit is 92.938% (computer simulation). 5. The odds of drawing seven dominos in any suit is 8 in 1,184,040 or 1 in 148,005. 6. Based on mathematical probability calculations (factorial equations). 7 Sep 2022: Thanks, Rich Burgardt, for correcting my overstated probability. -PP 7. The "cow" is the second highest domino in a suit, after the double. 8. Based on 100,000 computer simulated drawn hands (31,326 met criteria). 19 Dec 2010: Thanks, Zane, for reporting the original understated probability. -PP | ||
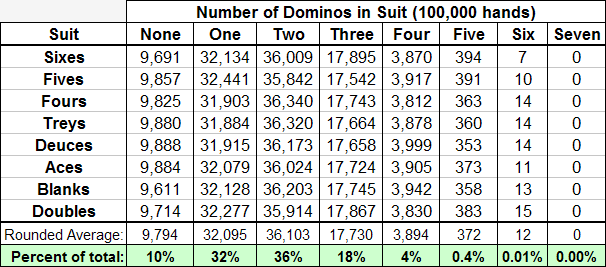
| Number of Dominos in a Given Suit | Odds of Drawing (Rounded) | Probability (Rounded) |
| None | 1 in 10 | 10% |
| One | 1 in 3 | 32% |
| Two | 1 in 3 | 36% |
| Three | 1 in 6 | 18% |
| Four | 1 in 25 | 4% |
| Five | 1 in 268 | 0.4% |
| Six | 1 in 8,055 | 0.01% |
| Seven | 1 in 1,184,040 | 0.0001% |
| Notes:
1. A hand is the initial seven dominos randomly drawn from a set of double-six dominos. 2. The number of possible combinations for drawing seven-domino hands is 1,184,040. 3. There are eight possible trump suits: blanks, aces, deuces, treys, ..., and doubles. 4. A "given" suit is a particular or specific suit, e.g., doubles can be a suit of their own. | ||
| I modified the script in my handy-dandy domino utility to automatically shuffle and draw 100,000 hands and tabulate the accumulated results. Here are the results for drawing specific suits (they agree with the calculated percentages in Table II above): |
| Here are the computer simulations for drawing combinations in any suit (tabulated in Table I above): |
|
Thanks to my wife, Joan, for doing the logic and factorial expressions for the combinations in doubles. And thanks to Dennis Roberson and Jerry Whitney for critiquing my work.
Also, on 6 August 2015, Jon Jerome provided the answer to this question: If two players are playing with a set of double-six dominos, and each draws seven bones, what are the odds that neither player has drawn a double? His answer, determined from 100,000 reiterations, was that the odds of neither player drawing a double are only 3/10 of one percent, or roughly once in every 333 drawings. (See subsequent calculations below that agree with Jon's computer reiterations.) Calculations contributed by Luis Flavio Nunes, 28 January 2019:If two players are playing with a set of double-six dominoes, and each draws seven bones, what are the odds that neither player has drawn a double?In the domino set, we have 7 doubles and 21 'simple' dominoes. So, as the 2 players will draw 14 dominoes in total, the number of possible combinations is: Comb. 28,14 = (28x27x...x15) / (14x13x...x2x1) = 40,116,600 Now, the number of favorable results, that is, the number of ways to draw 14 dominoes from the 21 'simple' ones, is: Comb. 21,14 = (21x20x...x8) / (14x13x...x2x1) = 116,280 The probability then is 116,280/40,116,600 = 1/345 or near 3/10 of one percent, like checked. |